题目内容
已知正比例函数y=kx与反比例函数y=| k | x |
分析：此题可直接将坐标代入函数解析式，再联立解方程即可求出另一个交点．
解答：解：正比例函数y=kx①与反比例函数y=
(k＞0)②的一个交点是（2，3），
∴将（2，3）代入①得k=
，代入②得k=6，即正比例函数y=
x③，反比例函数y=
④，
∴
x=
，解之得x=±2，把x=-2代入③得y=-3．
∴另一个交点是（-2，-3）．
故答案为：-2；-3．
| k |
| x |
∴将（2，3）代入①得k=
| 3 |
| 2 |
| 3 |
| 2 |
| 6 |
| x |
∴
| 3 |
| 2 |
| 6 |
| x |
∴另一个交点是（-2，-3）．
故答案为：-2；-3．
点评：本题考查函数与方程的应用，函数图象经过某点，则某点适合解析式，转化为方程求解．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
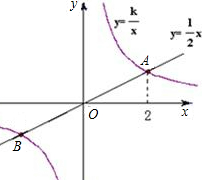横坐标为2．
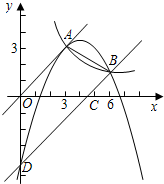如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．