题目内容
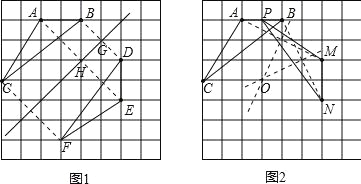
【题目】如图所示,在8×8的网格中,我们把△ABC在图1中作轴对称变换,在图2中作旋转变换,已知网格中的线段ED、线段MN分别是边AB经两种不同变换后所得的像,请在两图中分别画出△ABC经各自变换后的像,并标出对称轴和旋转中心(要求:不写作法,作图工具不限,但要保留作图痕迹).

【答案】作图参见解析.
【解析】
试题分析:(1)根据轴对称性质,对称轴是对应点所连线段的垂直平分线,先找到对称轴,连接BD和AE,分别取BD和AE的中点G,H,连接GH,则GH即为轴对称变换的对称轴,作点C关于GH的对称点,然后顺次连接各点即可;(2)先根据线段AB经旋转变换后得到MN,找出旋转中心和旋转方向,根据旋转性质,对应点到旋转中心的距离相等,分别连接AM,BN,作线段AM,BN的垂直平分线,两平分线的交点即为旋转中心,然后根据旋转规律找出旋转后的各点,顺次连接各点即可.
试题解析:(1)先找到对称轴,连接BD和AE,分别取BD和AE的中点G,H,连接GH,则GH即为轴对称变换的对称轴,作点C关于GH的对称点,然后顺次连接各点,所画图形如图1所示:其中GH为轴对称变换的对称轴,△DEF与△BAC关于直线GH对称;(2)分别连接AM,BN,作线段AM,BN的垂直平分线,两平分线的交点O即为旋转变换的旋转中心,连接CO,根据旋转角相等,找到C的对应点P,连接PMN,则△MNP由△ABC以点O为旋转中心,顺时针旋转90°得到.

练习册系列答案
相关题目