题目内容
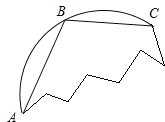
【题目】如图是一块残缺的圆轮片,点A、B、C在圆弧E上.
(1)画出![]() 所在的⊙O;
所在的⊙O;
(2)若AB=BC=60,∠ABC=120°,求![]() 所在⊙O的半径.
所在⊙O的半径.
【答案】(1)作图参见解析;(2)60.
【解析】
试题分析:(1)先找到圆心,利用尺规作图,作出线段AB和BC的垂直平分线,两垂直平分线的交点即为圆心O,以O为圆心,OA或OB或OC长为半径画圆,即为弧AC所在的圆O;(2)利用边边边判定三角形ABO和三角形BOC全等,从而算出∠CBO=60度,然后能判断出三角形BOC是等边三角形,进而求出圆O的半径.
试题解析:(1)如图所示:先找到圆心,利用尺规作图,作出线段AB和BC的垂直平分线,两垂直平分线的交点即为圆心O,以O为圆心,OA长为半径画圆,即为弧AC所在的圆O;
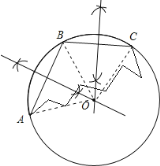 (2)如图,连接OA、OB、OC,∵AB=BC,AO=BO=CO, ∴△AOB≌△BOC,∠BAO=∠ABO=∠CBO=∠BCO, ∵∠ABC=120°,∴∠CBO=∠ABO=60°,∵BO=CO,∴∠OBC=∠BCO=60°,∴△OBC是等边三角形,∵BC=60,∴半径为60.
(2)如图,连接OA、OB、OC,∵AB=BC,AO=BO=CO, ∴△AOB≌△BOC,∠BAO=∠ABO=∠CBO=∠BCO, ∵∠ABC=120°,∴∠CBO=∠ABO=60°,∵BO=CO,∴∠OBC=∠BCO=60°,∴△OBC是等边三角形,∵BC=60,∴半径为60.

练习册系列答案
相关题目