题目内容
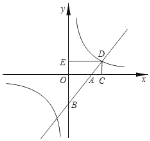
【题目】如图,直线y=x+b交x轴于A点,交y轴于B点,与反比例函数y= ![]() 交于点D,作DC⊥x轴,DE⊥y轴,则ADBD的值为________.
交于点D,作DC⊥x轴,DE⊥y轴,则ADBD的值为________.
【答案】4
【解析】
设D(x,y),由一次函数的性质知∠ABO=45°,从而AD=![]() OE,BD=
OE,BD=![]() BE,ADBD=2OEBE=2(y2﹣by),联立一次函数和反比例函数解析式可求y2﹣yb=2,进而可求出结论.
BE,ADBD=2OEBE=2(y2﹣by),联立一次函数和反比例函数解析式可求y2﹣yb=2,进而可求出结论.
解:设D(x,y)
∴OE=y,
∵y=x+b中,k=1,
∴∠ABO=45°,
∴∠OAB=45°,
∴AD=![]() OE,BD=
OE,BD=![]() BE,
BE,
∴ADBD=2OEBE,
∵令x=0代入y=x+b,
∴y=b,
∴B(0,b),
∴BE=y﹣b,
∴ADBD=2y(y﹣b)=2(y2﹣by),
∵点D在直线y=x+b与y=![]() 上,
上,
∴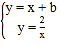 .
.
∴y2﹣yb=2,
∴ADBD=2×2=4,
故答案为4.

练习册系列答案
相关题目
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)