题目内容
【题目】（1）等腰三角形底边长为6cm，一腰上的中线把它的周长分成两部分的差为2cm，则腰长为________．
（2）已知
的周长为24，
，
于点D，若
的周长为20，则AD的长为________．
（3）已知等腰三角形的周长为24，腰长为x，则x的取值范围是________．
【答案】4cm或8cm 8 
【解析】
（1）根据题意画出图形，由题意得
，即可得
，又由等腰三角形的底边长为6cm，即可求得答案．
（2）由△ABC的周长为24得到AB，BC的关系，由△ABD的周长为20得到AB，BD，AD的关系，再由等腰三角形的性质知，BC为BD的2倍，故可解出AD的值．
（3）设底边长为y，再由三角形的三边关系即可得出答案．
（1）如图，
，BD是中线
由题意得存在两种情况：①②
①，
∵
∴
②，
∵
∴
∴腰长为：4cm或8cm
故答案为：4cm或8cm．
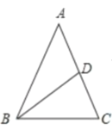
（2）∵△ABC的周长为24，
∴
∵
∴
∴
∴
∵
的周长为20
∴
∴
故答案为：8．
（3）设底边长为y
∵等腰三角形的周长为24，腰长为x
∴
∴
，即
解得
故答案为：．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
