题目内容
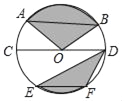
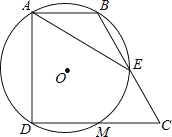
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,且CE=1,下列结论:①DM=CM;②![]() ;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
【答案】①②③④
【解析】
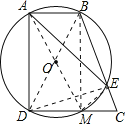
连接BD,BM,AM,EM,DE,由90度角所对的弦为直径,得到BD为圆的直径,再利用直径所对的圆周角为直角,得到∠BMD为直角,利用三个角为直角的四边形为矩形得到ADMB为矩形,利用矩形的对边相等得到AB=DM=1,而CD=2,得到CM=1,可得出M为DC的中点,即DM=CM,故选项①正确;由AB与MC平行且相等,利用一组对边平行且相等的四边形为平行四边形,得到四边形AMCB为平行四边形,可得出BE∥AM,由圆内平行线所夹的弧相等,得出![]() ,故选项②正确;由AM=BC,BD=AM,等量代换得到BC=BD,由BD为圆的直径,利用直径所对的圆周角为直角,得到△DEC为直角三角形,由DC与EC的长,利用勾股定理求出DE的长,设BE=x,则BD=BC=BE+EC=x+1,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,都等于DC的一半,用HL定理证明Rt△AEM≌Rt△ADM,即可对于选项④作出判断.
,故选项②正确;由AM=BC,BD=AM,等量代换得到BC=BD,由BD为圆的直径,利用直径所对的圆周角为直角,得到△DEC为直角三角形,由DC与EC的长,利用勾股定理求出DE的长,设BE=x,则BD=BC=BE+EC=x+1,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,都等于DC的一半,用HL定理证明Rt△AEM≌Rt△ADM,即可对于选项④作出判断.
解:(1)连接BD,BM,AM,EM,DE,
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ADMB矩形,
∴AB=DM=1,
又∵CD=2,
∴CM=1
∴DM=CM,
故①正确。
∵AB∥MC,AB=MC,
∴四边形AMCB是平行四边形,
∴BE∥AM,
∴![]() ,
,
故②正确。
∵AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又CE=1,CD=2,根据勾股定理得:DE=![]() =
=![]() ,
,
设BE=x,BD=BC=BE+EC=x+1,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+![]() =(x+1)2,
=(x+1)2,
解得:x=1,
∴BD=2,
故③正确;
∵![]() ,
,
∴AB=EM=1,
∴DM=EM,
∵∠ADM=90,
∴AM是直径,
∴∠AEM=∠ADM=90,
在Rt△AEM和Rt△ADM中,
![]() ,
,
∴Rt△AEM≌Rt△ADM(HL),
故选项④正确;
故答案为:①②③④