题目内容
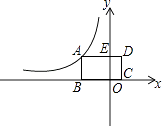
【题目】如图,已知抛物线l1经过原点与A点,其顶点是P(﹣2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
(1)点A的坐标是;抛物线l1的解析式是;
(2)当BM=3时,求b的值;
(3)把抛物线l1绕点(0,1)旋转180°,得到抛物线l2 .
①直接写出当两条抛物线对应的函数值y都随着x的增大而减小时,x的取值范围;
(4)②直线m与抛物线l2交于点N,设线段MN的长为n,求n与b的关系式,并求出线段MN的最小值与此时b的值.
【答案】
(1)(﹣4,0);y=﹣ ![]() (x+2)2+3
(x+2)2+3
(2)
解:在y=﹣ ![]() (x+2)2+3中,令y=﹣3,则﹣
(x+2)2+3中,令y=﹣3,则﹣ ![]() (x+2)2+3=﹣3,
(x+2)2+3=﹣3,
解得:x=﹣2 ![]() ﹣2或2
﹣2或2 ![]() ﹣2.
﹣2.
当在y=﹣ ![]() (x+2)2+3中,令y=3时,则﹣
(x+2)2+3中,令y=3时,则﹣ ![]() (x+2)2+3=3,
(x+2)2+3=3,
解得x=﹣2,即b=﹣2.
则b=﹣2或2 ![]() ﹣2或﹣2
﹣2或﹣2 ![]() ﹣2;
﹣2;
(3)﹣2<x<2
(4)
解:设M的坐标是(b,﹣ ![]() ),则N的坐标是(b,
),则N的坐标是(b, ![]() (b﹣2)2﹣1),
(b﹣2)2﹣1),
则MN= ![]() (b﹣2)2﹣1)﹣[﹣
(b﹣2)2﹣1)﹣[﹣ ![]() ]=
]= ![]() b2+2.
b2+2.
则当b=0时,MN最小,是2.
【解析】解:(1)∵顶点P的坐标是(﹣2,3),即对称轴是x=﹣2,
∴A的坐标是(﹣4,0).
设抛物线的解析式是y=a(x+2)2+3,
把(0,0)代入得4a+3=0,
解得a=﹣ ![]() ,
,
则抛物线的解析式是y=﹣ ![]() (x+2)2+3.
(x+2)2+3.
故答案是:(﹣4,0),y=﹣ ![]() (x+2)2+3.
(x+2)2+3.
·(3)P(﹣2,3)关于(0,1)的对称点是(2,﹣1),
则抛物线L2的解析式是y= ![]() (x﹣2)2﹣1,
(x﹣2)2﹣1,
①当﹣2<x<2时,两条抛物线对应的函数值y都随着x的增大而减小.
答案是:﹣2<x<2;
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案