题目内容
已知半径分别为m，n的两圆的圆心距为4，公切线的条数是3，则|1-m-n|的值为
- A.-3
- B.3
- C.5
- D.-5
B
分析：由公切线的条数是3，可知两圆外切，从而可知m+n=4，则1-m-n|=m+n-1=4-1=3．
解答：∵公切线的条数是3，
∴两圆外切，圆心距等于两圆半径之和，
∴m+n=4，
∴|1-m-n|=m+n-1=4-1=3．
故选B．
点评：本题利用了两圆外切时，有3条公切线的性质，两圆外切时，圆心距等于两圆半径之和．
分析：由公切线的条数是3，可知两圆外切，从而可知m+n=4，则1-m-n|=m+n-1=4-1=3．
解答：∵公切线的条数是3，
∴两圆外切，圆心距等于两圆半径之和，
∴m+n=4，
∴|1-m-n|=m+n-1=4-1=3．
故选B．
点评：本题利用了两圆外切时，有3条公切线的性质，两圆外切时，圆心距等于两圆半径之和．
练习册系列答案
阅读快车系列答案
相关题目
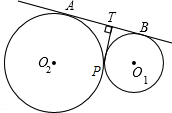已知半径分别为1和2的两个圆外切于点P，则点P到两圆外公切线的距离为