题目内容
【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= ![]() (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.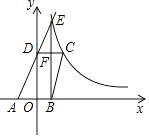
(1)若EB= ![]() OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
【答案】
(1)
解:∵C(2,3),
把C(2,3)代入y= ![]() 中,k=6,
中,k=6,
∴y= ![]() ,
,
∵CD⊥y轴,
∴OD=3,
∵BE= ![]() OD,
OD,
∴BE=4,
∴y=4时,4= ![]() ,
,
∴x= ![]() ,
,
∴点E坐标(2, ![]() )
)
(2)
解:设E(m, ![]() ),则B(m,0),
),则B(m,0),
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵DF∥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得m=1,
∴E(1,6),
设直线AD的解析式为y=kx+b,则有 ![]() ,
,
解得 ![]() ,
,
∴直线AD的解析式为y=3x+3.
【解析】(1)根据点C坐标求出反比例函数的解析式,再求出点E的纵坐标,即可解决问题.(2)设E(m, ![]() ),则B(m,0),由四边形ABCD是平行四边形,推出CD=AB=2,由DF∥AB,推出
),则B(m,0),由四边形ABCD是平行四边形,推出CD=AB=2,由DF∥AB,推出 ![]() =
= ![]() ,推出
,推出 ![]() =
= ![]() ,解得m=1,可得E(1,6),设直线AD的解析式为y=kx+b,利用待定系数法即可解决问题.
,解得m=1,可得E(1,6),设直线AD的解析式为y=kx+b,利用待定系数法即可解决问题.

 阅读快车系列答案
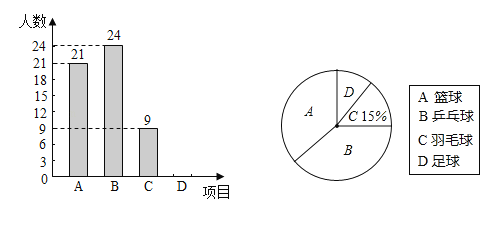
阅读快车系列答案【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表: 抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题: 
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?