��Ŀ����
����Ŀ����ɽ��ij��ѧΪ�ձ����ѧ���������ʣ���չÿ�조��������һСʱ���������ʵ�������������A������B��ƹ����C����ë��D�����������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ���˶���Ŀ�������ȡ��һ����ѧ�����е��飬ÿ��ѧ��������ֻ��ѡ����ϲ����һ���˶���Ŀ����������������������������������ͳ��ͼ������ͼ�е���Ϣ����������⣺
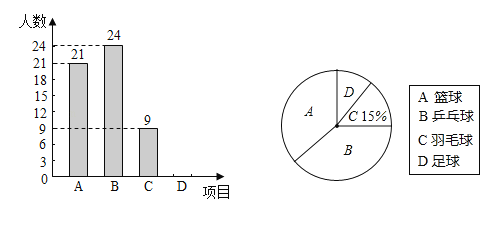
��1����α�����ѧ�����ˣ��벹ȫ����ͳ��ͼ��
��2����ͳ��ͼ�У���ƹ����Ӧ���ε�Բ�Ľ����ȣ�
��3��������ѧ����3600��ѧ����ϲ�������ѧ��Լ�ж����ˣ�
���𰸡���1��60��ͼ�������������2��144����3��1260.
��������
��1���������ͳ��ͼ������ͳ��ͼ������C������9����C����ռ����15%�����ɵõ���У���α������ѧ��������������������ȥA��B��C����������ɵ�D���������Ȼ��ȫ����ͳ��ͼ��
��2����B�����������������ٳ���360�����ɵõ�������
��3����3600���Գ�������ϲ�������˶���Ŀ��������ռ�İٷֱȼ�����
��1����ϲ����ë��C������9����ռ15%����������=9��15%=60���ˣ�����ϲ������D��������Ϊ��60����21+24+9��=6���ˣ�����ȫ����ͳ��ͼ������
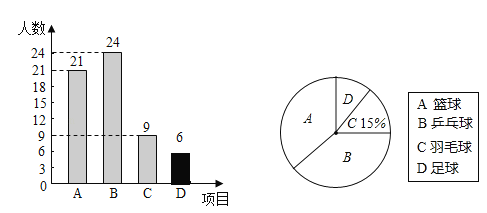
��2����ϲ��ƹ����B��������Ϊ24����������Ϊ60��������ƹ����Ӧ���ε�Բ�Ľ���360���![]() =144�㣻
=144�㣻
��3��3600��![]() =1260���ˣ���
=1260���ˣ���
��������ѧ����3600��ѧ����ϲ�������ѧ��Լ��1260�ˣ�