题目内容
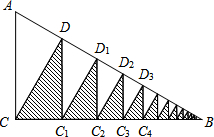 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2.作△ABC的高CD,作△CDB的高DC1,作△DC1B的高C1D1,…,如此下去,则得到的所有阴影三角形的面积之和为
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2.作△ABC的高CD,作△CDB的高DC1,作△DC1B的高C1D1,…,如此下去,则得到的所有阴影三角形的面积之和为3
| ||
| 7 |
3
| ||
| 7 |
分析:若逐一求阴影部分的面积此题会比较复杂,可从整体的角度来求解此题;易知所有白色部分的小直角三角形都与阴影部分的三角形相似,那么它们的面积比应该等于相似比的平方,它们的相似比为AC:CD,AC的长已知,根据直角三角形面积的不同表示方法可求得CD,由此求得阴影部分占△ABC面积的比例大小,从而可求得阴影部分的面积和.
解答: 解:∵DC1∥AC,
解:∵DC1∥AC,
∴Rt△ACD∽△CDC1,同理可证:Rt△C1D1D∽Rt△C1D1C2,…;
即白色部分的小直角三角形与阴影部分的小直角三角形逐一对应相似,
∵如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,
∴AB=2AC=4,BC=
=2
.
在Rt△ABC中,CD⊥AB,
由S=
AC•BC=
AB•CD,故CD=
,
∴AC:CD=2:
,
∴白色部分小直角三角形的面积和:阴影部分小直角三角形的面积和=AC2:CD2=4:3,
故S阴影=
S△ABC=
×
×2×
=
.
故答案是:
.
 解:∵DC1∥AC,
解:∵DC1∥AC,∴Rt△ACD∽△CDC1,同理可证:Rt△C1D1D∽Rt△C1D1C2,…;
即白色部分的小直角三角形与阴影部分的小直角三角形逐一对应相似,
∵如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,
∴AB=2AC=4,BC=
| AB2-AC2 |
| 3 |
在Rt△ABC中,CD⊥AB,
由S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴AC:CD=2:
| 3 |
∴白色部分小直角三角形的面积和:阴影部分小直角三角形的面积和=AC2:CD2=4:3,
故S阴影=
| 3 |
| 7 |
| 3 |
| 7 |
| 1 |
| 2 |
| 3 |
3
| ||
| 7 |
故答案是:
3
| ||
| 7 |
点评:此题主要考查了含30度角的直角三角形,勾股定理,以及相似三角形的判定和性质,注意整体思想在此题中的应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).