题目内容
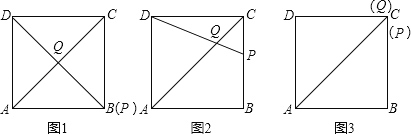
【题目】如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．
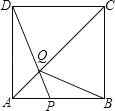
（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
（2）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P 运动到什么位置时，△ADQ恰为等腰三角形．
【答案】（1）证明见解析；（2）当点P运动到①点B的位置；②在BC上，且到点B的距离为8﹣4
处；③运动到点C的位置时，△ADQ恰为等腰三角形．
【解析】
试题分析：（1）根据正方形的四条边都相等可得AD=AB，对角线平分一组对角可得∠DAQ=∠BAQ=45°，然后利用“边角边”证明△ADQ和△ABQ全等；
（2）分①AQ=DQ时，点B、P重合，②AQ=AD时，根据等边对等角可得∠ADQ=∠AQD，再求出正方形的对角线AC的长，再求出CQ，然后根根据两直线平行，内错角相等求出∠CPQ=∠ADQ，从而得到∠CQP=∠CPQ，根据等角对等边可得CP=CQ，从而得到点P的位置，③AD=DQ时，点C、P、Q三点重合．
（1）证明：在正方形ABCD中，无论点P运动到AB上何处时，
都有AD=AB，∠DAQ=∠BAQ=45°，
在△ADQ和△ABQ中，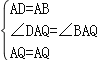
，
∴△ADQ≌△ABQ（SAS）；
（2）若△ADQ是等腰三角形，
则有①如图1，AQ=DQ时，点Q为正方形ABCD的中心，点B、P重合；
②如图2，AQ=AD时，根据等边对等角有∠ADQ=∠AQD，
∵正方形ABCD的边长为4，
∴AC=
=4
，
∴CQ=AC﹣AQ=4﹣4，
∵AD∥BC，
∴∠CPQ=∠ADQ，
∴∠CQP=∠CPQ，
∴CP=CQ=4﹣4，
此时点P在距离点B：4﹣（4﹣4）=8﹣4；
③如图3，AD=DQ时，点C、P、Q三点重合；
综上所述，当点P运动到①点B的位置；②在BC上，且到点B的距离为8﹣4处；③运动到点C的位置时，△ADQ恰为等腰三角形．
