题目内容
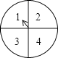
【题目】如图,转盘被划分成![]() 个相同的小扇形,并分别标上数字
个相同的小扇形,并分别标上数字![]() ,
,![]() ,
,![]() ,
,![]() ,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中
,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中![]() 点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点
点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点![]() 落在直线
落在直线![]() 的下方的概率为( )
的下方的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
用列表法,把点M的坐标的16种情况都表示出来,可知中落在直线y=x下方的有(2,1),(3,1),(4,1),(3,2),(4,2),(4,3),共6种,所以M点落在落在直线y=x下方的概率是![]() =
=![]() .
.
设M的坐标(x,y),
列表得:
x y | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
M点的坐标所有的情况有共16种,
则点(x,y)落在直线y=x下方的有(2,1),(3,1),(4,1),(3,2),(4,2),(4,3),共6种情况,
∴点(x,y)落在直线y=x下方的概率为![]() =
=![]() .
.
故答案选B.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目