题目内容
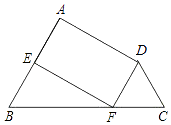
【题目】如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.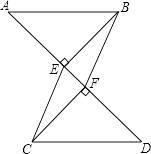
【答案】证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
∵AF=DE,
∴AE=DF,
在△AEB与△DFC中,
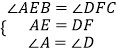 ,
,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
【解析】由BE⊥AD,CF⊥AD,得到∠AEB=∠DFC=90°,由AB∥CD得到∠A=∠D,再由AF=DE得到AE=DF,得到△AEB≌△DFC(ASA),得出BE=CF,再由BE⊥AD,CF⊥AD,得到BE∥CF,由四边形的定义判定四边形BECF是平行四边形.
【考点精析】通过灵活运用平行四边形的判定,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.

练习册系列答案
相关题目
【题目】用![]() 纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为![]() (
(![]() 为非负整数).
为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) |
| 2 | … | ||
乙复印店收费(元) |
|
| … |
(2)设在甲复印店复印收费![]() 元,在乙复印店复印收费
元,在乙复印店复印收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由.