题目内容
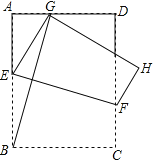
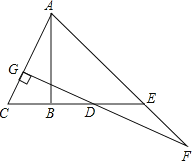
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.
【答案】(1)45°﹣α;(2)相等,理由见解析;(3)EF=3![]() .
.
【解析】
(1)根据等腰三角形的性质得到∠BAE=∠AEB=45°,根据三角形的内角和即可得到结论;
(2)连接AD,根据线段垂直平分线的性质得到AC=AD,求得∠ADC=∠ACB=α,于是得到AC=DF;
(3)根据已知条件得到BD=CB=3,过F作FH⊥CE交CE的延长线于H,得到△EHF是等腰直角三角形,求得FH=HE,根据全等三角形的性质即可得到结论.
解:(1)∵AB⊥CD,
∴∠ABE=90°,
∵AB=BE,
∴∠BAE=∠AEB=45°,
∵∠CAB=α,∠CDG=90°﹣(90°﹣α)=α=∠EDF.
∴∠AFG=∠AED﹣∠EDF=45°﹣α;
故答案为:45°﹣α;
(2)相等,
证明:连接AD,
∵AB垂直平分线段CD,
∴AC=AD,
∴∠ADC=∠ACB=90°﹣α,
∴∠DAE=∠ADC﹣45°=45°﹣α,
∴∠DAE=∠AFD,
∴AD=DF,
∴AC=DF;
(3)∵CD=6,
∴BD=CB=3,
过F作FH⊥CE交CE的延长线于H,
则△EHF是等腰直角三角形,
∴FH=HE,
∵∠H=∠ABC=90°,∠CAB=∠CDG=∠FDH,AC=AD=DF,
∴△ACB≌△DFH(AAS),
∴FH=CB=3,
∴EF=![]() FH=3
FH=3![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目