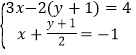题目内容
【题目】在直角坐标系中，正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上，点C1、C2、C3、…、Cn均在x轴上．若点B1的坐标为（1，1），点B2的坐标为（3，2），则点An的坐标为 ． 
【答案】（2n﹣1﹣1，2n﹣1）
【解析】解：∵B1的坐标为（1，1），点B2的坐标为（3，2）， ∴正方形A1B1C1O1边长为1，正方形A2B2C2C1边长为2，
∴A1的坐标是（0，1），A2的坐标是：（1，2），
代入y=kx+b得 
，
解得： 
．
则直线的解析式是：y=x+1．
∵A1B1=1，点B2的坐标为（3，2），
∴A1的纵坐标是1，A2的纵坐标是2．
在直线y=x+1中，令x=3，则纵坐标是：3+1=4=22；
则A4的横坐标是：1+2+4=7，则A4的纵坐标是：7+1=8=23；
据此可以得到An的纵坐标是：2n﹣1 ， 横坐标是：2n﹣1﹣1．
故点An的坐标为 （2n﹣1﹣1，2n﹣1）．
故答案是：（2n﹣1﹣1，2n﹣1）．
首先求得直线的解析式，分别求得A1 ， A2 ， A3…的坐标，可以得到一定的规律，据此即可求解．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
