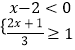��Ŀ����
����Ŀ��ij�������м���ԭ��360ǧ�ˣ�����ԭ��290ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ50��������һ��A��Ʒ��Ҫ����ԭ��9ǧ�ˣ�����ԭ��3ǧ�ˣ��ɻ�����700Ԫ������һ��B��Ʒ����Ҫ����ԭ��4ǧ�ˣ�����ԭ��10ǧ�ˣ��ɻ�����1200Ԫ��
��1��������x��A�ֲ�Ʒ��д��������xӦ����IJ���ʽ�飻
��2�����������ļ��ְ�Ҫ����A��B���ֲ�Ʒ��������������������������������Ƴ�����
���𰸡���1��![]() ����2����3����������������1��A��Ʒ30����B��Ʒ20��������2��A��Ʒ31����B��Ʒ19��������3��A��Ʒ32����B��Ʒ18����
����2����3����������������1��A��Ʒ30����B��Ʒ20��������2��A��Ʒ31����B��Ʒ19��������3��A��Ʒ32����B��Ʒ18����
����������������1��������x��A�ֲ�Ʒ��������B��Ʒ��50��x����������Ҫ����ԭ��[9x+4��50��x��]ǧ��������ԭ��[3x+10��50��x��]ǧ������������Ϳ��Խ�������ʽ����
��2�������1���IJ���ʽ��Ľ⼯���Ϳ���ȷ��x��ֵ���Ӷ��������������
�������1��������x��A�ֲ�Ʒ��������B��Ʒ��50��x����������Ҫ����ԭ��[9x+4��50��x��]ǧ��������ԭ��[3x+10��50��x��]ǧ�������������
![]() ��
��
��2����![]() �������30��x��32����x��������x=30��31��32������3������������
�������30��x��32����x��������x=30��31��32������3������������
����1��A��Ʒ30����B��Ʒ20����
����2��A��Ʒ31����B��Ʒ19����
����3��A��Ʒ32����B��Ʒ18����

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�