题目内容
【题目】已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )
A.![]()
cm2
B.![]()
cm2
C.![]()
cm2
D.![]()
cm2
【答案】A
【解析】解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2﹣BC2 ,
∴AC=4 ![]() cm,
cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4 ![]() cm,
cm,
∴S△ABC= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() cm2 ,
cm2 ,
设DO为x,则CO=x,则AO=BO=(4 ![]() ﹣x)cm,
﹣x)cm,
在Rt△COB中,CO2+BC2=BO2 ,
即:x2+42=(4 ![]() ﹣x)2
﹣x)2
∴D0= ![]() cm,
cm,
∴S△ADO= ![]() ×
× ![]() ×4=
×4= ![]() ,
,
∴S△AOB=S△ABC﹣S△ADO= ![]()
∵AB∥CD,
∴△AOB∽△DOC,
∴( ![]() )2=
)2= ![]()
∴S△DOC= ![]() ,
,
故选:A.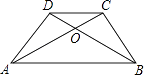
【考点精析】掌握等腰梯形的性质是解答本题的根本,需要知道等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.

【题目】鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查. 
通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
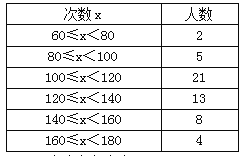
(1)请你补全下面的数据统计表: 家装风格统计表
装修风格 | 划记 | 户数 | 百分比 |
A中式 | 正正正正正 | 25 | 50% |
B欧式 | |||
C韩式 | 5 | 10% | |
D其他 | 正 | 10% | |
合计 | 50 | 100% |
(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)
(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?