题目内容
观察下列各式:1×3=12+2×1;
2×4=22+2×2;
3×5=32+2×3;……
请你将猜想到的规律用正整数n表示出来 。
2×4=22+2×2;
3×5=32+2×3;……
请你将猜想到的规律用正整数n表示出来 。

分析:根据题意可知1×3=12+2×1,2×4=22+2×23×5=32+2×3,4×6=42+2×4,所以n(n+2)=n2+2n。
解答:
∵1×3=12+2×1,
2×4=22+2×2,
3×5=32+2×3,
4×6=42+2×4,
∴n(n+2)=n2+2n.
点评:主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
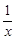 +
+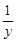 +
+ =0,那么x2+y2+z2的值为 。
=0,那么x2+y2+z2的值为 。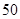 元的乘车IC卡,如果他乘车的次数用
元的乘车IC卡,如果他乘车的次数用 表示,则记录他每次乘车后的余额
表示,则记录他每次乘车后的余额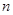 (元)如下表:
(元)如下表: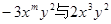 是同类项,则m等于( ).
是同类项,则m等于( ).