题目内容
如果x+y+z=a,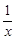 +
+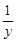 +
+ =0,那么x2+y2+z2的值为 。
=0,那么x2+y2+z2的值为 。
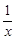 +
+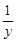 +
+ =0,那么x2+y2+z2的值为 。
=0,那么x2+y2+z2的值为 。a2
由题意将x+y+z=a,两边平方,然后再根据条件 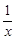 +
+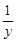 +
+ =0,得出xy+xz+yz=0,从而求出x2+y2+z2的值.
=0,得出xy+xz+yz=0,从而求出x2+y2+z2的值.
解:∵x+y+z=a,
∴(x+y+z)2=x2+y2+z2+2xy+2xz+2yz,
又∵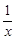 +
+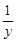 +
+ =0,
=0,
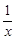 +
+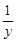 +
+ =
=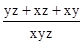 ,
,
∴xy+xz+yz=0,
∴(x+y+z)2=x2+y2+z2+2xy+2xz+2yz=a2,
故答案为:a2.
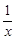 +
+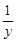 +
+ =0,得出xy+xz+yz=0,从而求出x2+y2+z2的值.
=0,得出xy+xz+yz=0,从而求出x2+y2+z2的值.解:∵x+y+z=a,
∴(x+y+z)2=x2+y2+z2+2xy+2xz+2yz,
又∵
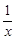 +
+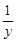 +
+ =0,
=0,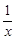 +
+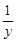 +
+ =
=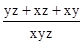 ,
,∴xy+xz+yz=0,
∴(x+y+z)2=x2+y2+z2+2xy+2xz+2yz=a2,
故答案为:a2.

练习册系列答案
相关题目

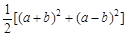
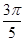 x2y3z的次数是______.
x2y3z的次数是______. 米(窗框的宽度忽略不计),那么窗框的面积是 ( )
米(窗框的宽度忽略不计),那么窗框的面积是 ( )
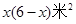

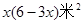
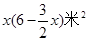
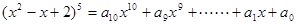 ,则
,则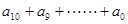 =_________。
=_________。 ,其中
,其中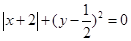 .
.