题目内容
对下列多项式分解因式正确的是（ ）
a3b2－a2b3+a2b2=a2b2(a－b) B、4a2－4a+1=4a(a－1)+1
C、a2+4b2=(a+2b)2 D、1－9a2=(1+3a)(1－3a)
a3b2－a2b3+a2b2=a2b2(a－b) B、4a2－4a+1=4a(a－1)+1
C、a2+4b2=(a+2b)2 D、1－9a2=(1+3a)(1－3a)
D
分析：根据因式分解的定义，把一个多项式写成几个整式积的形式叫做因式分解，并根据提取公因式法，利用完全平方公式与平方差公式法分解因式对各选项分析判断后利用排除法．
解：A、a3b2-a2b3+a2b2=a2b2（a-b+1），故本选项错误；
B、4a2-4a+1=（2a-1）2，故本选项错误；
C、a2+4b2不能分解因式，故本选项错误；
D、1-9a2=（1+3a）（1-3a），利用了平方差公式，故本选项正确．
故选D．
解：A、a3b2-a2b3+a2b2=a2b2（a-b+1），故本选项错误；
B、4a2-4a+1=（2a-1）2，故本选项错误；
C、a2+4b2不能分解因式，故本选项错误；
D、1-9a2=（1+3a）（1-3a），利用了平方差公式，故本选项正确．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
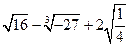
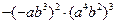
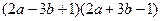
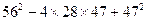
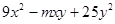是一个完全平方式，则
的值为（ ）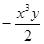
的同类项___________________________.
那么
.
，其中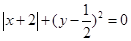
.