题目内容
【题目】已知抛物线y=ax2+bx+c的图像如图所示,则下列结论:
①abc>0;②a+b+c=2;③b>1;④a< ![]() .
.
其中正确的结论是( )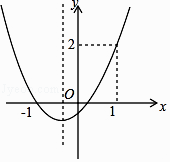
A.①②
B.②③
C.③④
D.②④
【答案】B
【解析】解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x= ![]() <0,∴a、b同号,即b>0,
<0,∴a、b同号,即b>0,
∴abc<0,
故本选项错误;
②当x=1时,函数值为2,
∴a+b+c=2;
故本选项正确;
③当x=﹣1时,函数值<0,
即a﹣b+c<0,(1)
又a+b+c=2,
将a+c=2﹣b代入(1),
2﹣2b<0,
∴b>1
故本选项正确;
④∵对称轴x=- ![]() >﹣1,
>﹣1,
解得: ![]() <a,
<a,
∵b>1,
∴a> ![]() ,
,
故本选项错误;
综上所述,其中正确的结论是②③;
故选B.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】小文同学每天乘从BRT(城市快速公交)上学,为了方便乘坐BRT,他用自己勤工俭学的钱买了80元的公交卡.如果他乘坐的次数用n表示,则记录他每次乘坐BRT后公交卡的余额(单位:元)如下表:
次数n | 余额(元) |
1 | 80-0.9 |
2 | 80-1.8 |
3 | 80-2.7 |
4 | 80-3.6 |
… | … |
(1)写出用乘坐BRT的次数n表示余额的式子为____________________;
(2)利用(1)中的式子,帮助小文同学算一算,他一个月乘坐BRT有84次,这80元的公交卡够不够用,若够用,能剩多少元?
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次.