Question

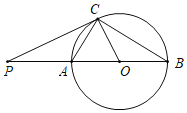
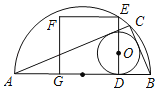
【题目】如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆上．

（1）当正方形的顶点F也在半圆弧上时，半圆的半径与正方形边长的比为　 　；

（2）当正方形DEFG的面积为100，且△ABC的内切圆⊙O的半径r＝4，求半圆的直径AB的值；

（3）若半圆的半径为R，直接写出⊙O半径r可取得的最大值．

Answer 1

【答案】（1）；（2）AB＝21；（3）

【解析】

（1）根据圆和正方形的对称性可知：，在直角三角形FGH中，利用勾股定理可得，从而用含a的代数式表示半圆的半径为，正方形边长为2a，所以可求得半圆的半径与正方形边长的比；

（2）切点分别为I，J，连接EB、AE，OJ、OI，可得OJCI是正方形，且边长是4，可设BD＝x，AD＝y，则BD＝BJ＝x，AD＝AI＝y，分别利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作为相等关系列方程组求解即可求得半圆的直径AB＝21．

（3）根据（2）中得出方程解答即可．

解：（1）如图，根据圆和正方形的对称性可知：，

H为半圆的圆心，

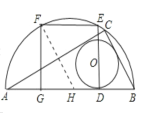
不妨设GH＝a，则GF＝2a，

在直角三角形FGH中，由勾股定理可得，由此可得，半圆的半径为，正方形边长为2a，

所以半圆的半径与正方形边长的比是；

（2）因为正方形DEFG的面积为100，所以正方形DEFG边长为10．

切点分别为I，J，连接EB、AE，OI、OJ，

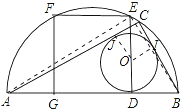
∵AC、BC是⊙O的切线，

∴CJ＝CI，∠OJC＝∠OIC＝90°，

∵∠ACB＝90°，

∴四边形OICJ是正方形，且边长是4，

设BD＝x，AD＝y，则BD＝BI＝x，AD＝AJ＝y，

在直角三角形ABC中，由勾股定理得（x+4）2+（y+4）2＝（x+y）2①；

在直角三角形AEB中，

∵∠AEB＝90°，ED⊥AB，

∴△ADE∽△BDE∽△ABE，

∴ 即ED2＝ADBD，即102＝xy②．

解①式和②式，得x+y＝21，

即半圆的直径AB＝21；

（3）由（2）可得：，

当点C与点E重合且为半圆弧的中点时，⊙O半径r可取得的最大值为．