��Ŀ����
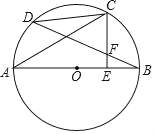
����Ŀ����ͼ1����ABC�͡�CDE���ǵȱ������Σ��ҵ�A��C��E��һ��ֱ���ϣ�AD��BE���ڵ�O��AD��BC���ڵ�P��CD��BE���ڵ�Q������PQ
��1����֤��AD��BE��
��2����AOB�Ķ���Ϊ�� ����PQ��AE��λ�ù�ϵ���� ����
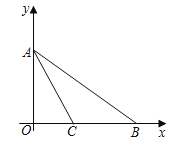
��3����ͼ2����ABC�̶�������CDE�Ƶ�C��˳ʱ�루����ʱ�룩������ת����Ƕ���������ת�����У���1���еĽ����Ƿ��ܳ�������AOB�Ķ����Ƿ�ı䣿��˵�����ɣ�

���𰸡���1������������2��60�㣬PQ��AE����3������ת�����У���1���еĽ����ܳ�������AOB�Ķ�������ı䣬������
��������
��1�����ݵȱ����������ʵó�AC��BC��CE��CD����ACB����ECD��60���������BCE����ACD������SAS�Ƴ���������ȫ�ȼ��ɣ�
��2���������ε�������ʣ��ɵá�AOB����BEA+��DAC����ACB����EBC+��BEA�����AOB����ACB��60����֤����QPC����BCA���ɵ�PQ��AE��
��3��֤����ACD�ա�BCE��SAS�����õ�AD��BE����DAC����EBC�����ݡ�BOA��180������ABO����BAO��180������ABC����BAC�����ɽ��
��1��֤�����ߡ�ABC�͡�CDEΪ�ȱ������Σ�
��AC��BC��CD��CE����BCA����DCE��60����
���ACD����BCE��
�ڡ�ACD�͡�BCE�У�
AC��BC����ACD����BCE��CD��CE��
���ACD�ա�BCE��SAS����
��AD��BE��
��2���ߡ�ACD�ա�BCE��
���DAC����EBC��
�������ε�������ʣ���AOB����BEA+��DAC��
��ACB����EBC+��BEA��
���AOB����ACB��60����
�ߡ�DCP��60������ECQ��
���ڡ�CDP�͡�CEQ�У�
��ADC����BEC��CD��CE����DCP����ECQ��
���CDP�ա�CEQ��ASA����
��CP��CQ��
���CPQ����CQP��60������PCQ�ǵȱ������Σ�
���QPC����BCA��
��PQ��AE��
�ʴ�Ϊ��60����PQ��AE��
��3������ת�����У���1���еĽ����ܳ�������AOB�Ķ�������ı䣬�������£�
�ߡ�ABC�͡�CDE���ǵȱ������Σ�
��AC��BC��CD��CE����ACB����DCE��60����
���ACB+��BCD����DCE+��BCD��
����ACD����BCE��
�ڡ�ACD�͡�BCE�У�
��AC=BC����ACD=��BCE��CD=CE��
���ACD�ա�BCE��SAS����
��AD��BE����DAC����EBC��
���BOA��180������ABO����BAO��180������ABC����BAC��60����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ����ѧ���ϣ�����ʦ��ʾ�����¿��е���Ŀ��
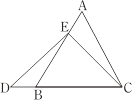
�ڵȱ�������ABC�У���E��AB�ϣ���D��CB���ӳ����ϣ���ED=EC����ͼ����ȷ���߶�AE��DB�Ĵ�С��ϵ����˵�����ɣ� |
|
С����ͬ��С�����ۺ��������½��
��1�����������̽������
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE���DB��С��ϵ������ֱ��д�����ۣ�
AE DB(�����������������)��

ͼ1 ͼ2
��2�����������������Ŀ
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE DB(�����������������)��
�������£���ͼ2������E��EF��BC����AC�ڵ�F.
(����������½�����)
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC������ABC�ı߳�Ϊ1��AE=2����CD�ij�(����ֱ��д�����)��