题目内容
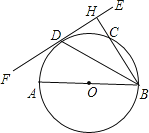
【题目】如图![]() ,在
,在![]() 中,
中,![]() 是原点,
是原点,![]() 是
是![]() 的角平分线.
的角平分线.
![]() 确定
确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出
轴的距离相等,若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 在线段
在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到点
到点![]() 和点
和点![]() 的距离相等,若存在,直接写出点
的距离相等,若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
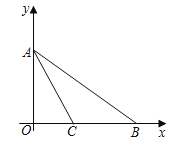
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)存在,,
;(3)存在,,![]()
【解析】
(1)设![]() 的表达式为:
的表达式为: ![]() ,将A、B的坐标代入即可求出直线AB的解析式;
,将A、B的坐标代入即可求出直线AB的解析式;
(2)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() ,然后根据勾股定理求出AB,利用
,然后根据勾股定理求出AB,利用![]() 即可求出点C的坐标,利用待定系数法求出AC的解析式,设
即可求出点C的坐标,利用待定系数法求出AC的解析式,设![]() ,代入解析式中即可求出点P的坐标;
,代入解析式中即可求出点P的坐标;
(3)根据AC的解析式设点Q的坐标为(b,![]() ),然后利用平面直角坐标系中任意两点之间的距离公式求出QA和QB,然后利用QA=QB列方程即可求出点Q的坐标.
),然后利用平面直角坐标系中任意两点之间的距离公式求出QA和QB,然后利用QA=QB列方程即可求出点Q的坐标.
![]() 由题意得,设
由题意得,设![]() 的表达式为:
的表达式为: ![]()
将![]() 代入得,
代入得,
![]()
解得:
![]()
![]() 存在
存在
过点![]() 作
作![]() 交
交![]() 于
于![]()

![]() 是角平分线
是角平分线
![]()
在Rt△AOB中,![]()
由题意得
![]()
即有![]()
解得![]()
∴点C的坐标为:![]()
设直线AC的表达式为![]()
将![]() 代入,得
代入,得
![]()
解得:![]()
![]() 的表达式为
的表达式为![]()
设![]() ,代入
,代入![]() 得,
得,![]()
![]()
![]() 存在
存在
点Q在AC上,设点Q的坐标为(b,![]() )
)
∴QA=![]() ,
,
QB=![]()
∵QA=QB
∴![]()
解得:b=![]()
∴![]()

练习册系列答案
相关题目