Question

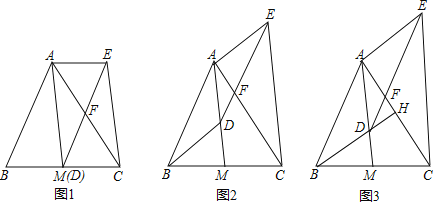
【题目】如图 1，在 Rt△ABC 中，∠ACB＝90°，AC＝BC，D 是 BC 上的一点，过点 D 作 DE⊥AB，垂足为点 E，F 为 AD 的中点，连接 CF、EF．

（1）猜想CF与EF的关系，并说明理由；

（2）如图2，连接BF，若∠AEF＝30°，求∠BFE 的度数．

Answer 1

【答案】(1)CF=EF，CF⊥EF，理由见解析；(2)∠BFE=15°.

【解析】

(1)由等腰直角三角形的性质可得∠CAB=∠EBD=45°，在Rt△ACD中，由直角三角形斜边中线的性质可得CF=AF，从而有∠FAC=∠FCA，同理在Rt△AED中，可得EF=AF，∠FAE=∠FEA，继而可得CF=EF，再由三角形外角的性质以及角的和差可得∠CFD+∠EFD=90°，即可得CF⊥EF；

(2)由∠EBD=45°，∠BED=90°可得BE=ED，再由∠AEF=30°，可得∠BEF=150°，∠FED=60°，继而可得△FED是等边三角形，从而有EF=ED，继而可得BE=EF，再利用等边对等角即可求得答案.

(1)CF=EF，CF⊥EF，理由如下：

∵Rt△ABC 中，∠ACB＝90°，AC＝BC，

∴∠CAB=∠B=45°，

∵DE⊥AB，

∴∠BED=∠AED=90°，

在Rt△ACD中，∠ACD=90°，F为AD中点，

∴CF=AF，

∴∠FAC=∠FCA，

在Rt△AED中，∠AED=90°，F为AD中点，

∴EF=AF，

∴∠FAE=∠FEA，

∴CF=EF，

∵∠CFD=∠FAC+∠FCA，∠EFD=∠FAE+∠FEA，∠FAC+∠FAE=∠CAB=45°，

∴∠CFD+∠EFD=90°，

即∠EFC=90°，

∴CF⊥EF；

(2)∵∠EBD=45°，∠BED=90°，

∴∠EDB=90°-∠EBD=45°=∠EBD，

∴BE=ED，

∵∠AEF=30°，

∴∠BEF=180°-∠AEF=150°，∠FED=∠AED-∠AEF=90°-30°=60°，∠FAE=∠AEF=30°，

∴∠ADE=60°，

∴∠FDE=∠FED=60°，

∴△FED是等边三角形，

∴EF=ED，

∴BE=EF，

∴∠BFE=(180°-150°)÷2=15°.