题目内容
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.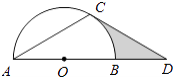
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
【答案】
(1)证明:连接OC. 
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC= ![]() .
.
在Rt△OCD中,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴ ![]() .
.
∴图中阴影部分的面积为: ![]()
![]() .
.
【解析】(1)要证CD是⊙O的切线,点C在半圆上,因此连接OC,需证明OC⊥CD。先根据等腰三角形的性质及三角形内角和定理求出∠2=∠A=∠D=30°.再求出∠OCD的度数,就可证出结论。
(2)根据图形分析阴影部分的面积=Rt△OCD的面积-扇形COB的面积,根据题意易求出∠1的度数,再利用解直角三角形求出CD的长,然后求出Rt△OCD的面积和扇形COB的面积,即可求得结果。

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量(m3) | 38 | 36 | 34 | 32 | … |
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?


