题目内容
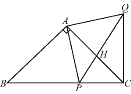
【题目】把一张矩形纸片ABC的按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F. 
(1)试在图中连接BE,求证:四边形BFB′E是菱形;
(2)若AB=8,BC=16,求线段BF长能取到的整数.
【答案】
(1)证明:连接BB′,如图1所示:
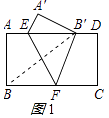
由折叠知点B、B′关于EF对称,
∴EF是线段BB′的垂直平分线,
∴BE=B′E,BF=B′F,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠B′EF=∠BFE,
由折叠得:∠B′FE=∠BFE,
∴∠B′EF=∠B′FE,
∴B′E=B′F,
∴BE=B′E=B′F=BF,
∴四边形BFB′E是菱形
(2)解:如图2所示:当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,
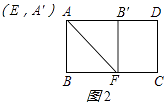
∵四边形ABFB′是正方形,
∴BF=AB=8,即BF最小为8;
如图2所示:当点B与点D重合时,BF最大,
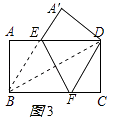
设BF=x,则CF=16﹣x,DF=BF=x,
在Rt△CDF中,由勾股定理得:CF2+CD2=DF2,
∴(16﹣x)2+82=x2,
解得:x=10,即BF=10,
∴8≤BF≤10,
∴线段BF长能取到的整数值为8,9,10.
【解析】(1)连接BB′,由折叠知点B、B′关于EF对称,得出EF是线段BB′的垂直平分线,证出BE=B′E,BF=B′F,由矩形的性质得出∠B′EF=∠BFE,由折叠得:∠B′FE=∠BFE,得出∠B′EF=∠B′FE,证出B′E=B′F,BE=B′E=B′F=BF,即可得出结论;(2)当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,由正方形的性质得出BF=AB=8,得出BF最小为8; 当点B与点D重合时,BF最大,设BF=x,则CF=16﹣x,DF=BF=x,在Rt△CDF中,由勾股定理得出方程,解方程求出BF=10,得出8≤BF≤10,即可得出结果.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数