题目内容
【题目】如图,在四边形ABCD中,AD∥BC,AD=BC,点F是AB的中点,点E是BC边上的点,DE=AD+BE,△DEF 的周长为l.
(1)求证:DF 平分∠ADE;
(2)若 FD=FC,AB=2,AD=3,求l的值.

【答案】(1)见解析;(2)8.
【解析】
(2)延长BF交CB延长线于点H,先证△ADE≌△HCE得AD=HB、DF=HF,
AD+BE=HB+BE=HE,结合DE=AD+BE得∠FDE=∠H,,根据∠ADF=∠H即可得证;
(3)先证∠BCD=90°得出DE =CE+CD =(3-BE)+2 =(3+BE),据此求得BE的长,从而得出CE的长度,进而得出答案.
(1)延长BF交CB延长线于点H,
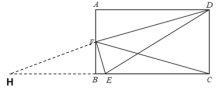
∵AD∥BC,
∴∠ADF=∠H,∠DAB=∠HBA,
∵F为AB的中点,
∴AF=BF,
∴△ADF≌△HBF,
∴AD=HB、DF=HF,
∴AD+BE=HB+BE=HE,
∵DE=AD+BE,∴DE=HE,
∴∠FDE=∠H,
又∵∠ADF=∠H,
∴∠FDE=∠ADF,
∴DF 平分∠ADE;
(2)∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD,
∵FD=HF、FD=FC,
∴FD=HF=FC,
∴∠FDC=∠FCD,∠H=∠HCF,
∵∠ADF=∠H,
∴∠ADF+∠FDC=∠HCF+∠FCD,即∠ADC=∠BCD,
∵AD∥BC, ∠ADC+∠BCD =180°,
∴∠BCD=90°,
∴DE =CE+CD =(3-BE)+2 =(3+BE),
解得:BE=![]() ,
,
∴DE=3+![]() =
=![]() ,CE=3-
,CE=3-![]() =
=![]() ,
,
∴△DEF的周长l=![]() =8.
=8.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目