题目内容
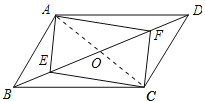
【题目】如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.

【答案】(1)证明见解析;(2)是,理由见解析;(3)不是.
【解析】试题分析:本题考查了平行四边形的性质与判定、菱形的性质与判定、矩形的性质;熟练掌握平行四边形、矩形、菱形的性质、并能进行推理论证是解决问题的关键.
(1)连接AC交BD于点O,由平行四边形的性质得出OA=OC,OE=OF,再证出OB=OD,即可得出结论;
(2)由菱形的性质得出AC⊥BD,即可得出结论;
(3)由矩形的性质得出OA=OC=OE=OF,证出OB=OD,AC<BD,得出四边形ABCD是平行四边形,不是矩形.
试题解析:(1)证明:连接AC交BD于点O,如图所示:
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形; ]
(2)解:理由如下:
∵四边形AECF是菱形,
∴AC⊥BD,
由(1)知,四边形ABCD是平行四边形;
∴四边形ABCD是菱形;
(3)解:四边形ABCD不是矩形;理由如下:
∵四边形AECF是矩形,
∴OA=OC,OE=OF,AC=EF,
∴OA=OC=OE=OF,
∵BE=DF,
∴OB=OD,
∴AC<BD,
∴四边形ABCD是平行四边形,不是矩形.

练习册系列答案
相关题目