题目内容
【题目】如图,△ABC中,∠C=90°,边AB的垂直平分线交AB、AC边分别为点D,点E,连结BE. 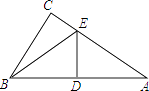
(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的周长.
【答案】
(1)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE=40°,
∵Rt△ABC中,∠C=90°,∠A=40°,
∴∠ABC=50°,
∴∠CBE=∠ABC﹣∠ABE=10°
(2)解:∵∠C=90°,AB=10,BC=6,
∴AC=8,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AC=8,
∴△BCE的周长=BE+CE+BC=AC+BC=14
【解析】(1)由AB的垂直平分线DE交AC于点E,可得AE=BE,继而求得∠ABE的度数,然后由Rt△ABC中,∠C=90°,求得∠ABC的度数,继而求得答案;(2)根据勾股定理得到AC=8,根据线段的垂直平分线的性质得到AE=BE,即可得到结论.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行了有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会. 在一个纸盒里装有2个红求和2个白球,除颜色外其他都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表)
甲 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 5 | 10 | 5 |
乙 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 10 | 5 | 10 |
(1)用树状图或列表法表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.