��Ŀ����
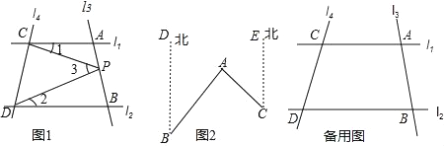
����Ŀ��̽�����֣���ͼ1����ֱ֪��l1��l2����l3��l1��l2�ֱ��ཻ��A��B���㣬l4��l1��l2�ֱ���C��D���㣬��ACP������1����BDP������2����CPD������3����P���߶�AB�ϣ�
��1������1=20�㣬��2=30�㣬���������3�Ķ���
�����ܽ��2����������������⣬�����ҳ�ͼ1�С�1����2����3֮���������ϵ����ֱ��д����Ľ��ۣ�
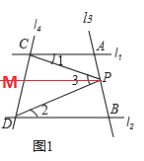
ʵ��Ӧ�ã���3��Ӧ�ã�2���еĽ��۽���������⣺��ͼ2����A��B�ı�ƫ��40��ķ����ϣ���C�ı�ƫ��45��ķ����ϣ����������������ֱ��д����BAC�Ķ�����
��չ���죺��4�������P��ֱ��l3������A��B��������˶�ʱ�������������䣬��̽����1����2��
��3֮��Ĺ�ϵ����P��A��B���㲻�غϣ���д����Ľ��۲�˵�����ɣ�
���𰸡���1��500����2����1+��2=��3����3��850����4����P����A�����ʱ����CPD=��2����1����P����B�����ʱ����CPD=��1����2��
�������������������1����P��PM��l1����ͼ��ʾ����l1��l2���õ�PM��l2�����ɵ���1=��CPM=20�㣬��2=��DPM=30�㣬������3=��CPM+��DPM=��1+��2=50�㣻��2����1+��2=��3����ȣ�1�����ɵý��ۣ���3����ȣ�1���ķ�����⼴�ɣ�(4)�ֵ�P����A������뵱P����B���������������з������ۼ���.
���������
��1��500 ��
��2����1+��2=��3��
��3��850
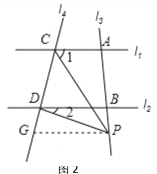
��4����P����A�����ʱ����ͼ1����P��PF��l1����l4��F��
���1=��FPC����l1��l4����PF��l2�����2=��FPD
�ߡ�CPD=��FPD����FPC
���CPD=��2����1��
��P����B�����ʱ����ͼ2����P��PG��l2����l4��G��
���2=��GPD ��l1��l2�� ��PG��l1��
���1=��CPG
�ߡ�CPD=��CPG����GPD
���CPD=��1����2��


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�