题目内容
【题目】如图,在平行四边形ABCD中,点G是线段AB上一点,连接CG、DG,满足CG=CD.
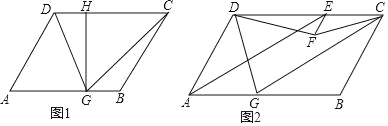
(1)如图1,过点G作GH⊥CD于点H,若AB=7,GH=2![]() ,求DG;
,求DG;
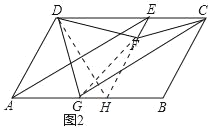
(2)如图2,若∠DAB=60°,∠DAB的角平分线交CD于点E,过点E作EF∥AD,满足EF+AG=AD,连接DF、CF,求证:∠DCF=∠GCF.
【答案】(1)DG=2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由平行四边形的性质和已知条件得出CG=CD=7,由勾股定理得出CH=![]() =5,得出DH=CD-CH=2,再由勾股定理即可得出结果;
=5,得出DH=CD-CH=2,再由勾股定理即可得出结果;
(2)延长EF交AB于H,连接DH、FG,先证明四边形ADEH是平行四边形,再由平行线的性质和角平分线证出∠AED=∠DAE,得出AD=ED,证出四边形ADEH是菱形,得出AD=ED=EH=AH,得出△ADH、△DEH是等边三角形,得出∠DHA=∠EDH=∠DEH=60°,DH=AD=DE,证出EF=GH,证明△DEF≌△DHG得出∠EDF=∠HDG,DF=DG,证出∠GDF=60°,得出△GDF是等边三角形,得出DF=GF,再证明△CDF≌△CGF,即可得出∠DCF=∠GCF.
(1)∵四边形ABCD是平行四边形,
∴CD=AB=7,
∵CG=CD=7,GH=2![]() ,BH⊥CD,
,BH⊥CD,
∴CH=![]() =
=![]() =5,
=5,
∴DH=CD﹣CH=2,
∴DG=![]() =2
=2![]() ;
;
(2)延长EF交AB于H,连接DH、FG,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EAB,
∵EF∥AD,
∴四边形ADEH是平行四边形,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠AED=∠DAE,
∴AD=ED,
∴四边形ADEH是菱形,
∴AD=ED=EH=AH,
∵∠DAB=60°,
∴△ADH、△DEH是等边三角形,
∴∠DHA=∠EDH=∠DEH=60°,DH=AD=DE,
∵EF+AG=AD=AH=AG+GH,
∴EF=GH,
在△DEF和△DHG中,
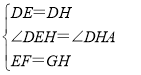 ,
,
∴△DEF≌△DHG(SAS),
∴∠EDF=∠HDG,DF=DG,
∴∠HDG+∠FDH=∠EDF+∠FDH=∠EDH=60°,即∠GDF=60°,
∴△GDF是等边三角形,
∴DF=GF,
在△CDF和△CGF中,
 ,
,
∴△CDF≌△CGF(SSS),
∴∠DCF=∠GCF.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案