题目内容
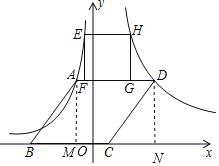
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点B,C在x轴上,反比例函数y=﹣![]() (x<0)的图象经过A,E两点,反比例函数y=
(x<0)的图象经过A,E两点,反比例函数y=![]() (x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(1)求点C的坐标及k的值;
(2)直接写出正方形EFGH的边长.

【答案】(1)点C坐标为(1,0),k=6;(2)2![]() ﹣2
﹣2
【解析】
(1)将A(﹣1,a)代入y=﹣![]() 中,得a=4.求得点A的坐标为(﹣1,4),过点A作AM⊥x轴于点M,过点D作DN⊥x轴于点N,根据勾股定理得到A B=
中,得a=4.求得点A的坐标为(﹣1,4),过点A作AM⊥x轴于点M,过点D作DN⊥x轴于点N,根据勾股定理得到A B=![]() =
=![]() =5,结合四边形ABCD是菱形,求得点C坐标为(1,0),点D坐标为(4,4),把点D(4,4)代入y=
=5,结合四边形ABCD是菱形,求得点C坐标为(1,0),点D坐标为(4,4),把点D(4,4)代入y=![]() 中,于是得到结论;
中,于是得到结论;
(2)设正方形EFGH的边长为a,得到E(﹣![]() ,a+4),得到H(
,a+4),得到H(![]() ,a+4),根据正方形的性质列方程解得a=2
,a+4),根据正方形的性质列方程解得a=2![]() ﹣2,(负值舍去).于是得到结论.
﹣2,(负值舍去).于是得到结论.
(1)将A(﹣1,a)代入y=﹣![]() 中,得a=4.
中,得a=4.
∴点A的坐标为(﹣1,4),
过点A作AM⊥x轴于点M,过点D作DN⊥x轴于点N,
∴∠A MB=∠DNC=90°,
∴AM∥DN.
则MO=1,AM=4.
∵点B(﹣4,0),
∴OB=4,BM=BO﹣MO=3.
在Rt△ABM中,A B=![]() =
=![]() =5,
=5,
∴四边形ABCD是菱形,
∴AD∥BC,AD=BC=AB=5,四边形AMND是矩形,
∴MN=AD=5, DN=AM=4,OC=BC﹣BO=5﹣4=1,ON=MN﹣M0=5﹣1=4.
∴点C坐标为(1,0),点D坐标为(4,4),
把点D(4,4)代入y=![]() 中,得k=16;
中,得k=16;
(2)设正方形EFGH的边长为a,
则∵E点反比例函数y=﹣![]() (x<0)的图象上,
(x<0)的图象上,
∴E(﹣![]() ,a+4),
,a+4),
∵H点在y=![]() 的图象上,
的图象上,
∴H(![]() ,a+4),
,a+4),
∴![]() ﹣(﹣
﹣(﹣![]() )=a,
)=a,
解得:a=2![]() ﹣2,(负值舍去).
﹣2,(负值舍去).
∴正方形EFGH的边长为2![]() ﹣2.
﹣2.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁