��Ŀ����
����Ŀ������̽��
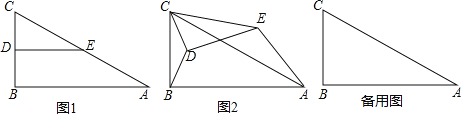
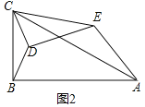
��ͼ1����Rt��ABC�У���B��90����AB��4��BC��2����D��E�ֱ��DZ�BC��AC���е㣬����DE������CDE�Ƶ�C��ʱ�뷽����ת������ת��Ϊ����
��1�����ⷢ��
��������0��ʱ��![]() ���� ������������180��ʱ��
���� ������������180��ʱ��![]() ���� ����
���� ����
��2����չ̽��
���жϣ���0�������360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3��������
��CDE�Ƶ�C��ʱ����ת��A��B��E������ͬһ��ֱ����ʱ�����߶�BD�ij���
���𰸡���1����![]() ����
����![]() ��2����0�������360��ʱ��
��2����0�������360��ʱ��![]() �Ĵ�Сû�б仯��3��BD�ij�Ϊ
�Ĵ�Сû�б仯��3��BD�ij�Ϊ![]() ��
��![]()
��������
��1���ٵ�����0��ʱ�����D��E�ֱ��DZ�BC��AC���е㣬��DE��BA���������ɵõ��𰸣��ڵ�����180��ʱ�����D��E�ֱ��DZ�BC��AC���ӳ����ϣ���DE��BA����![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��2���������߶�Ӧ�ɱ����Ҽн���ȵ��������������ƣ����ɵõ����ۣ�
��3��������������ۣ��ٵ���E��AB���ӳ�����ʱ�� �ڵ���E���߶�AB��ʱ�� ���![]() ��
��![]() ���ֱ�����𰸣����ɣ�
���ֱ�����𰸣����ɣ�
��1���١���Rt��ABC�У���B��90����AB��4��BC��2��
��![]() ��
��
������0��ʱ�����D��E�ֱ��DZ�BC��AC���е㣬
��DE��BA��
��![]() ������
������![]() ��
��
�ʴ��ǣ�![]() ��
��
�ڵ�����180��ʱ�����D��E�ֱ��DZ�BC��AC���ӳ����ϣ���DE��BA��
��![]() =
=![]() ��
��
�� ![]() ��
��
�ʴ��ǣ�![]() ��
��
��2����ͼ2����0�������360��ʱ��![]() �Ĵ�Сû�б仯���������£�
�Ĵ�Сû�б仯���������£�
�ߡ�ECD����ACB��
���ECA����DCB��
�ߵ�D��E�ֱ��DZ�BC��AC���е㣬����CD=1��CE=![]() ��
��
��![]() =
=![]() =
=![]() ��
��
����ECA����DCB��
��![]() =
=![]() =
=![]() ��
��
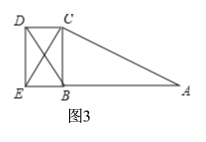
��3���ٵ���E��AB���ӳ�����ʱ����ͼ3��
��Rt��BCE��CE��![]() ��BC��2��
��BC��2��
��BE��![]() ��
��![]() ��1��
��1��
��AE��AB+BE��5��
��![]() ��
��![]() ��
��
��BD��![]() ��
��![]() ��
��
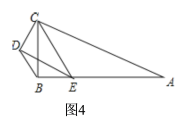
�ڵ���E���߶�AB��ʱ����ͼ4��
��BC=2��CE=![]() ����ABC=90�㣬
����ABC=90�㣬
��BE��1��AE��4��1��3��
��![]() ��
��![]() ��
��
��BD��![]() ��
��
��������������������BD�ij�Ϊ![]() ��
��![]() ��
��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�