题目内容
【题目】如图，
的面积是12，点D、E、F、G分别是BC、AD、BE、CE的中点，则四边形AFDG的面积是( )
A. 4.5B. 5C. 5.5D. 6
【答案】D
【解析】
根据中线的性质，可得△AEF的面积=
×△ABE的面积=
×△ABD的面积=
×△ABC的面积=
，同理可求出其他三角形面积，进而得到四边形AFDG的面积．
解：∵点D，E，F，G分别是BC，AD，BE，CE的中点，
∴AD是△ABC的中线，BE是△ABD的中线，CE是△ACD的中线，AF是△ABE的中线，AG是△ACE的中线，
∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积，
∴△AEF的面积=×12=，同理可得△AEG的面积=△DEF的面积=△DEG的面积=
∴四边形AFDG的面积=△AEF的面积+△AEG的面积+△DEF的面积+△DEG的面积=×4=6，
故选：D．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：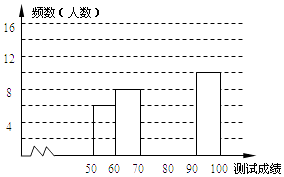
请结合图表完成下列各题：
（1）①表中a的值为 ， 中位数在第组；
②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
组别 | 成绩x分 | 频数（人数） |
第1组 | 50≤x＜60 | 6 |
第2组 | 60≤x＜70 | 8 |
第3组 | 70≤x＜80 | 14 |
第4组 | 80≤x＜90 | a |
第5组 | 90≤x＜100 | 10 |
