题目内容
【题目】已知x=﹣m和x=m﹣2时,多项式ax2+bx+4a+1的值都相等,且m≠1,若当1<x<2时,存在x的值,使多项式ax2+bx+4a+1的值为3,则a的取值范围是_____.
【答案】![]()
【解析】
利用x=-m和x=m-2时,ax2+bx+4a+1的值相等求出a、b的关系.在1<x<2范围内ax2+bx+4a+1的值在为3可等价于函数y=ax2+2ax+4a-2与x轴交点在1<x<2范围内,利用二次函数图象与性质看出x=1与x=2时,对应函数值的正负性,进而列出不等式求a的范围.
∵x=﹣m和x=m﹣2时,ax2+bx+4a+1的值相等
∴a(﹣m)2+b(﹣m)+4a+1=a(m﹣2)2+b(m﹣2)+4a+1
整理得:(4a﹣2b)(m﹣1)=0
∵m≠1
∴4a﹣2b=0,即b=2a
∵当1<x<2时,存在x使得ax2+bx+4a+1=3
∴a≠0
整理得:ax2+2ax+4a﹣2=0
令y=ax2+2ax+4a﹣2=a(x+1)2+3a﹣2
即抛物线y=a(x+1)2+3a﹣2与x轴的交点在1<x<2的范围内
①当a>0,如图1,在对称轴直线x=﹣1右侧y随x增大而增大
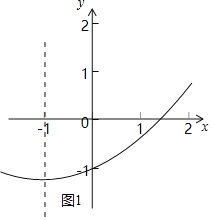
∴x=1时,y=a+2a+4a﹣2<0,解得:a<![]()
x=2时,y=4a+4a+4a﹣2>0,解得:a>![]()
∴![]() <a<
<a<![]()
②当a<0,如图2,在对称轴直线x=﹣1右侧y随x增大而减小
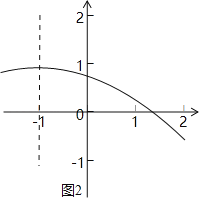
∴x=1时,y=a+2a+4a﹣2>0,解得:a>![]()
x=2时,y=4a+4a+4a﹣2<0,解得:a<![]()
∴不等式组无解
故答案为:![]() <a<
<a<![]() .
.

【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
![]() ______,
______,![]() ______.
______.
![]() 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.
![]() 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
![]() 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.