题目内容
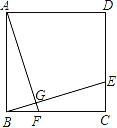
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.求证:BE=CF.

【答案】见解析
【解析】
连接BD,CD,由AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,根据角平分线的性质,即可得DE=DF,又由DG⊥BC且平分BC,根据线段垂平分线性质得∠BGD=∠CGD=90°,BG=CG,
再证△BGD≌△CGD(SAS), BD=CD.可得Rt△BED≌Rt△CFD(HL),BE=CF.
如图,连接BD,CD,
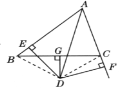
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
又∵DG⊥BC且平分BC,
∴∠BGD=∠CGD=90°,BG=CG,
在△BGD和△CGD中,

∴△BGD≌△CGD(SAS),
∴BD=CD.
在Rt△BED和Rt△CFD中,
![]()
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.

练习册系列答案
相关题目