Question

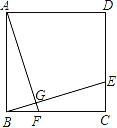
【题目】如图，在正方形ABCD中，点E，F分别在CD，BC上，且AF=BE，BE与AF相交于点G，则下列结论中错误的是（　　）

A. BF=CE B. ∠DAF=∠BEC

C. AF⊥BE D. ∠AFB+∠BEC=90°

Answer 1

【答案】D

【解析】

根据正方形的性质可得∠FBA=∠BCE=90°、AB=BC，结合BF=CE可用“SAS”得到△ABF≌△BCE，从而可对A进行判断；

由全等三角形的性质可得∠BAF=∠CBE，结合等角的余角相等即可对B进行判断；

由直角三角形的两个锐角互余可得∠BAF+∠AFB=90°，结合全等三角形的性质等量代换可得∠CBE+∠AFB=90°，从而可得到∠BGF的度数，据此对C进行判断；

对于D，由全等三角形的性质可知∠AFB=∠BEC，因此∠AFB=∠BEC=45°时D正确，分析能否得到∠AFB=45°即可对其进行判断.

∵四边形ABCD为正方形，

∴∠FBA=∠BCE=90°，AB=BC，

又∵AF=BE，

∴△ABF≌△BCE，

∴BF=CE，∠BAF=∠CBE.

故A正确；

∵∠C=90°，

∴∠CBE+∠BEC=90°.

∵∠BAD=∠BAF+∠DAF=90°，∠BAF=∠CBE，

∴∠DAF=∠BEC，故B正确.

∵∠BAF=∠CBE，∠BAF+∠AFB=90°，

∴∠CBE+∠AFB=90°，

∴∠BGF=90°，

∴AG⊥BE，故C正确.

∵△ABF≌△BCE，

∴∠AFB=∠BEC.

又∵点F在BC上，

∴∠AFB≠45°，

∴∠AFB+∠BEC≠90°，故D错误；

故选D.