Question

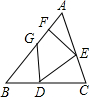如图，已知△ABC的面积为S，D是边BC的三等分点，E是边AC的四等分点，F，G皆是边AB的五等分点．则四边形DEFG的面积是

 

．

Answer 1

分析：连接CF、CG、AD，根据题目中给出的已知条件，分别求出S_△AEF、S_△BDG、和S_△DEC的面积，已知△ABC的面积为S，即可求出四边形DEFG的面积．

解答：解：如图，连接CF、CG、AD，

则S_△AEF=S×

1

5

×

3

4

=

3

20

S，
S_△BDG=S×

3

5

×

1

3

=

1

5

S，
S_△DEC=S×

2

3

×

1

4

=

1

6

S，
故S_{四边形DEFG}=S-（

3

20

S+

1

5

S+

1

6

S）=

29

60

S．
故填：

29

60

S．

点评：此题主要考查学生对三角形面积的理解和掌握，解答此题的关键的是连接CF、CG、AD，并根据题目中给出的已知条件，分别求出则S_△AEF、S_△BDG、和S_△DEC的面积．