Question

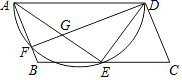
【题目】如图，在平行四边形ABCD中，E为BC边上的一点，且AE与DE分别平分∠BAD和∠ADC

（1）求证：AE⊥DE；
（2）设以AD为直径的半圆交AB于F，连结DF交AE于G，已知CD=5，AE=8．
①求BC的长；
②求 值．

Answer 1

【答案】
（1）

证明：在平行四边形ABCD中，∵AB∥CD，

∴∠BAD+∠ADC=180°．

又∵AE、DE平分∠BAD、∠ADC，

∴∠DAE+∠ADE=90°，

∴∠AED=90°，

∴AE⊥DE

（2）

解：①在平行四边形ABCD中，∵AD∥BC，AB=CD=5，AD=BC，

∴∠DAE=∠BEA，

又∵AE平分∠BAD，即∠DAE=∠BAE，

∴∠BEA=∠BAE，

∴BE=AB=5，

同理EC=CD=5，

∴BC=BE+EC=10，

②∵AD=BC=10，AE=8，

在Rt△AED中，DE= = =6，

又∵AE是∠BAD的角平分线，

∴∠FAG=∠DAE，

∵AD是直径，

∴∠AFD=90°，

∴tan∠FAG= ，

∴ =tan∠DAE= = = ．

【解析】（1）由∠BAD+∠ADC=180°．又因为AE、DE平分∠BAD、∠ADC，推出∠DAE+∠ADE=90°，即可推出∠AED=90°，由此即可解决问题．（2）①只要证明BA=BW，CD=CE即可解决问题．②由tan∠FAG= ，可得 =tan∠DAE= ，求出DE即可解决问题．