题目内容
【题目】如图，⊙M的圆心M（﹣1，2），⊙M经过坐标原点O，与y轴交于点A，经过点A的一条直线l解析式为：y=﹣ 
x+4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（﹣4，0）．
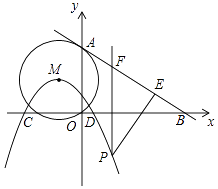
（1）求抛物线的解析式；
（2）求证：直线l是⊙M的切线；
（3）点P为抛物线上一动点，且PE与直线l垂直，垂足为E，PF∥y轴，交直线l于点F，是否存在这样的点P，使△PEF的面积最小？若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．
【答案】
（1）
解：设抛物线的解析式为y=a（x﹣2）（x+4），将点M的坐标代入得：﹣9a=2，解得：a=﹣ 
．
∴抛物线的解析式为y=﹣ x2﹣ 
x+ 
（2）
解：连接AM，过点M作MG⊥AD，垂足为G．
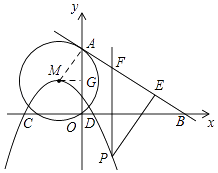
把x=0代入y=﹣ 
x+4得：y=4，
∴A（0，4）．
将y=0代入得：0=﹣ x+4，解得x=8，
∴B（8，0）．
∴OA=4，OB=8．
∵M（﹣1，2），A（0，4），
∴MG=1，AG=2．
∴tan∠MAG=tan∠ABO= ．
∴∠MAG=∠ABO．
∵∠OAB+∠ABO=90°，
∴∠MAG+∠OAB=90°，即∠MAB=90°．
∴l是⊙M的切线
（3）
解：∵∠PFE+∠FPE=90°，∠FBD+∠PFE=90°，
∴∠FPE=∠FBD．
∴tan∠FPE= ．
∴PF：PE：EF= 
：2：1．
∴△PEF的面积= PEEF= × 
PF 
PF= 
PF2．
∴当PF最小时，△PEF的面积最小．
设点P的坐标为（x，﹣ x2﹣ x+ ），则F（x，﹣ x+4）．
∴PF=（﹣ x+4）﹣（﹣ x2﹣ x+ ）=﹣ x+4+ x2+ x﹣ = x2﹣ 
x+ 
= （x﹣ 
）2+ 
．
∴当x= 时，PF有最小值，PF的最小值为 ．
∴P（ ， 
）．
∴△PEF的面积的最小值为= ×（ ）2= 
【解析】（1）设抛物线的解析式为y=a（x﹣2）（x+4），将点M的坐标代入可求得a的值，从而得到抛物线的解析式；（2）连接AM，过点M作MG⊥AD，垂足为G．先求得点A和点B的坐标，可求得，可得到AG、ME、OA、OB的长，然后利用锐角三角函数的定义可证明∠MAG=∠ABD，故此可证明AM⊥AB；（3）先证明∠FPE=∠FBD．则PF：PE：EF= ：2：1．则△PEF的面积= PF2 ， 设点P的坐标为（x，﹣ x2﹣ x+ ），则F（x，﹣ x+4）．然后可得到PF与x的函数关系式，最后利用二次函数的性质求解即可．
【考点精析】利用二次函数的性质对题目进行判断即可得到答案，需要熟知增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
