��Ŀ����
����Ŀ���ס������������˿�������10������Ϸ����Ϸ�������£�
��������������Ϊ���������������6��������������6������������ƵĻ�ɫ�أ���
���������ƽ���ʱ���������Ƶ�����������ӣ�����������֮��С�ڻ����10����ʱ��������֮�;��������յ�����������������֮�ʹ���10���������յ�������0��
����Ϸ����֮ǰ˫������֪���Է�����������
���ж���Ϸ����������ǣ������յ��������һ����ʤ�������յ��������ʱ����ʤ����
�ּס��Ҿ��������������ƣ�����֮�Ͷ���5����ʱ���ϻ������ű��泯�ϵ��˿��ƣ��������ֱַ���4��5��6��7��

��1�����״����ϼ�����һ���˿��ƣ��Ҳ������ƣ����ʤ�ĸ���Ϊ ��
��2�������ȴ����ϼ�����һ���˿��ƣ������Ҵ�ʣ�µ��˿���������һ���ƣ�Ȼ��˫���������ƣ�������״ͼ������ʾ��������ƺ����п��ܵĽ�������б����ּס��ҵ������յ������������һ�ʤ�ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
�������������������1��������4��5�ɻ�ʤ������6��7���һ�ʤ�����ɵõ���ʤ�ĸ��ʣ�
��2��������״ͼ�����ɵó����ۣ�
�����������1��������4��5�ɻ�ʤ������6��7���һ�ʤ����P����ʤ��=![]() =
=![]() ��
��
��2����ͼ��
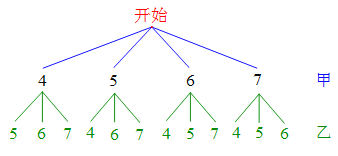
�����п��ܵĽ���ǣ�4��5����4��6����4��7����5��4����5��6����5��7����6��4����6��5����6��7��
��7��4����7��5����7��6�� ��12�֣�
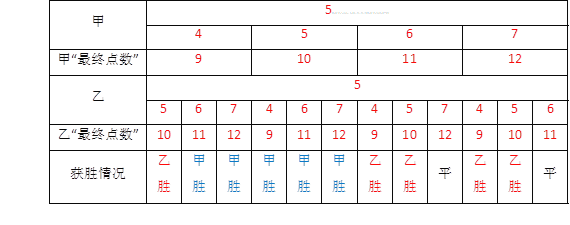
��P���һ�ʤ��=![]() ��
��

����Ŀ����ͼ�������ң���ÿ��С���Ӷ�����һ��������ʹ�����������������ڸ�������������֮�Ͷ���ȣ�
|
|
|
|
|
|
|
��![]() �������
�������![]() __________����
__________����![]() �������е���Ϊ__________��
�������е���Ϊ__________��
��![]() ���жϣ�ǰ
���жϣ�ǰ![]() ����������������֮���Ƿ����Ϊ
����������������֮���Ƿ����Ϊ![]() �����ܣ����
�����ܣ����![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�
��![]() �����
�����![]() ��
��![]() Ϊǰ���������е���������������ô���е�
Ϊǰ���������е���������������ô���е�![]() �ĺͿ���ͨ�����㣺
�ĺͿ���ͨ�����㣺
![]() �õ�����
�õ�����![]() ��
�� ![]() Ϊǰ
Ϊǰ![]() �������е������������������е�
�������е������������������е�![]() �ĺ�Ϊ__________��
�ĺ�Ϊ__________��
