Question

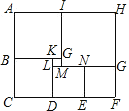
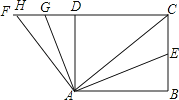
【题目】如图，在矩形ABCD中，AC是对角线，点E是BC的中点，连接AE，AB=4，BC=3，将∠BAE绕点A逆时针旋转，使∠BAE的两边分别与线段CD的延长线相交于点G，H．当AH=AC时，CG= ．

Answer 1

【答案】．

【解析】

试题分析：设∠BAE=∠GAH=α，∠DAG=β，由四边形ABCD是矩形，得到∠B=90°，根据勾股定理得到AE==，由三角函数的定义得到sinα=，cosα=，sin（α+β）=，cos（α+β）==，根据两角和和两角差的正余弦公式求得cosβ=，sinβ=，于是得到tanβ===，即可得到结论．

解：设∠BAE=∠GAH=α，∠DAG=β，

∵四边形ABCD是矩形，

∴∠B=90°，

∴AE==，

∴sinα=，cosα=，

∴sin（α+β）=，cos（α+β）==，

∴cosβ=cos（α+β﹣α）=cos（α+β）cosα+sin（α+β）sinβ=×+=，

sinβ=sin（α+β﹣α）=sin（α+β）cosα﹣cos（α+β）sinα=，

∴tanβ===，

∴DG=ADtanβ=3×=，

∴CG=4+=．

故答案为：．