Question

【题目】如图，已知大长方形ACFH的面积为572，被分割成六个小正方形，设最小的正方形边长a，第二小的正方形边长为b．

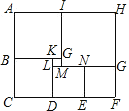
（1）a与b的关系为 ；

（2）求a．

Answer 1

【答案】（1）b=4a；（2）2

【解析】

试题分析：（1）表示出其余正方形的边长，根据最大正方形边长的两种表示方法相等可得a与b的关系；

（2）先求出矩形的长和宽，根据矩形ACFH的面积等于572列方程求解即可．

解：（1）AC=BC+AB=b+a+（b+2a）=2b+3a，

CF=EF+DE+CD=2b+（b+a）=3b+a，

最大正方形可表示为2b﹣a，也可表示为b+3a，

2b﹣a=b+3a，

解得b=4a．

故a与b的关系为b=4a．

（2）AB=11a，BC=13a，

矩形的面积为11a×13a=572，

a2=4，

解得a=±2（负值舍去）．

故答案为：b=4a．