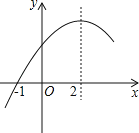题目内容
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(注:凸四边形就是没有角度数大于180°的四边形,把四边形的任何一边向两方延长,其他各边都在延长所得直线的同一旁,这样的四边形叫做凸四边形.)

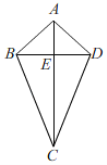
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有_________;②在凸四边形![]() 中,
中,![]() 且
且![]() ,则该四边形_________“十字形”.(填“是”或“不是”)
,则该四边形_________“十字形”.(填“是”或“不是”)
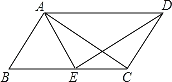
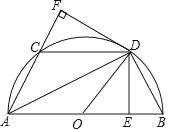
(2)如图1,![]() ,
,![]() ,
,![]() ,
,![]() 是半径为1的
是半径为1的![]() 上按逆时针方向排列的四个动点,
上按逆时针方向排列的四个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图2,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() ,
,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线与
是抛物线与![]() 轴的交点,点
轴的交点,点![]() 的坐标为
的坐标为![]() ,记“十字形”
,记“十字形”![]() 的面积为
的面积为![]() ,记
,记![]() ,
,![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() .求同时满足下列三个条件的抛物线的解析式:①
.求同时满足下列三个条件的抛物线的解析式:①![]() ;②
;②![]() ;③“十字形”
;③“十字形”![]() 的周长为
的周长为![]() .
.
【答案】(1)①菱形,正方形;②不是;(2)![]() (
(![]() );(3)
);(3)![]() .
.
【解析】
(1)①根据十字形的定义结合平行四边形,矩形,菱形,正方形对角线的性质进行判断;
②假设当![]() 时,根据SSS定理证得
时,根据SSS定理证得![]() ,然后结合全等三角形的性质求得
,然后结合全等三角形的性质求得![]() ,从而根据题意判断四边形
,从而根据题意判断四边形![]() 不是“十字形”;
不是“十字形”;
(2)先根据圆周角定理求得![]() ,然后过点
,然后过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,结合垂径定理和勾股定理求得
,结合垂径定理和勾股定理求得![]() ,然后根据题意列不等式组求解即可;
,然后根据题意列不等式组求解即可;
(3)由二次函数的性质求求得,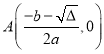 ,
,![]() ,
,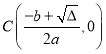 ,
,![]() ,然后结合三角形面积分别求得
,然后结合三角形面积分别求得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,然后根据题意列等式分别求得a,b的值,从而判断四边形
,然后根据题意列等式分别求得a,b的值,从而判断四边形![]() 是菱形,利用菱形性质求解c,求得抛物线解析式.
是菱形,利用菱形性质求解c,求得抛物线解析式.
解:(1)①∵菱形,正方形的对角线互相垂直,
∴菱形,正方形是:“十字形”,
∵平行四边形,矩形的对角线不一定垂直,
∴平行四边形,矩形不是“十字形”,
故答案为:菱形,正方形;
②如图,
当![]() 时,在
时,在![]() 和
和![]() 中,
中,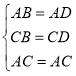 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 不是“十字形”,
不是“十字形”,
故答案为:不是;
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如图1,过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,
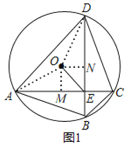
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (
(![]() );
);
(3)由题意得,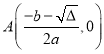 ,
,![]() ,
,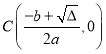 ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴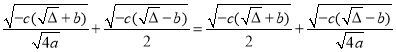 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍),
(舍),
即:![]() .
.