题目内容
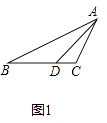
【题目】已知，如图①，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，点P为线段BC上的一动点（不运动到C，B两点）过点P作PQ⊥BC交AB于点Q，在AC边上取一点D，使QD=QP，连结DP，设CP=x
（1）求QP的长，用含x的代数式表示．
（2）当x为何值时，△DPQ为直角三角形？
（3）记点D关于直线PQ的对称点为点D′．
①当点D′落在AB边上时，求x的值；
②在①的条件下，如图②，将此时的△DPQ绕点P顺时针旋转一个角度α（0°＜α＜∠DPB），在旋转过程中，设DP所在的直线与直线AB交于点M，与直线AC交于点N，是否存在这样的M，N两点，使△AMN为等腰三角形？若存在，求出此时AN的长；若不存在，请说明理由．
【答案】
（1）
解：如图1中，
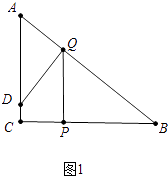
∵PQ⊥BC，
∴∠QPB=∠C=90°，
∴PQ∥AC，
∴ 
= 
，
∴ 
= 
，
∴PQ= 
（4﹣x）
（2）
解：因为△DPQ为直角三角形，由题意只有∠DQP=90°，如图2中，
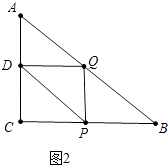
∵∠DQP=∠C=∠QPC=90°，
∴四边形PCDQ是矩形，
∵DQ=PQ，
∴四边形PCDQ是正方形，
∵∴PQ∥AC，
∴ = ，
∴ 
= ，
∴x= 
，
∴当x= 时，△PDQ是直角三角形．
（3）
解：①当点D′落在AB边上时，如图3中，设PQ与DD′交于点H．作 
于M．
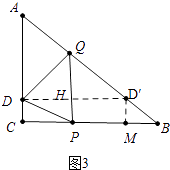
∵∠QHD′=∠C=90°，∠HD′Q=∠B，
∴△QHD′∽△ACB，
∴ 
= 
，
∵D′M∥AC，
∴ 
= 
，
∴ 
= 
，
∴D′M=3﹣ 
x，
∴QH=PQ﹣PH=3﹣ x﹣3+ x= x，
∴ 
= 
，
∴x= ．
∴x= 时，点D′落在AB边上．
②由题意只有旋转到如图位置时，△AMN是等腰三角形，此时AN=AM．
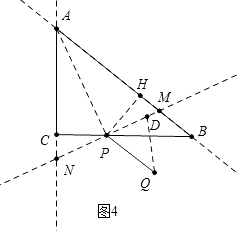
作PH⊥AB于H，
∵PC= ，
∴PB=BC﹣PC=4﹣ = 
，
∵sin∠ABC= 
= 
，
∴ 
= 
，
∴PH= ，
∴PC=PH，∵PC⊥AC，PH⊥AB，
∴PA平分∠BAC，
∵AN=AM，
∴AP⊥MN，
∵∠PAC=∠PAN，∠ACP=∠APN，
∴△ACP∽△APN，
∴ 
= 
，
∴ 
= 
，
∴AN= 
．
【解析】（1）由PQ∥AC，得 = ，列出方程即可解决问题．（2）因为△DPQ为直角三角形，由题意只有∠DQP=90°，如图2中，首先证明四边形PCDQ是正方形，由PQ∥AC，得 = ，列出方程即可解决问题．（3）①当点D′落在AB边上时，如图3中，设PQ与DD′交于点H．作 于M．由△QHD′∽△ACB，得 = 
，由D′M∥AC，得到 = ，求出D′M，列出方程即可解决问题．
②由题意只有旋转到如图位置时，△AMN是等腰三角形，此时AN=AM．首先证明PA平分∠BAC，再根据△ACP∽△APN，得 = ，列出方程即可解决问题．
【考点精析】本题主要考查了比例的性质的相关知识点，需要掌握基本性质；更比性质（交换比例的内项或外项）；反比性质（交换比的前项、后项）；等比性质才能正确解答此题．
