题目内容
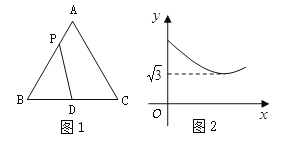
【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP= ![]() ,PD=
,PD= ![]() ,若
,若![]() 与
与![]() 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
【答案】D
【解析】从图2的函数图象为抛物线得知,y与x满足二次函数关系,同时y的最小值为![]() ,结合等边三角形的图形可知,当点P运动到DP⊥AD位置时,DP长为最小值,利用等边三角形的特殊角可求出边长,从而得出等边三角形ABC的面积.
,结合等边三角形的图形可知,当点P运动到DP⊥AD位置时,DP长为最小值,利用等边三角形的特殊角可求出边长,从而得出等边三角形ABC的面积.
解:由图二可得y最小值=![]() ,
,
∵△ABC为等边三角形,分析图一可知,当P点运动到DP⊥AB时,DP长为最小值,
∴此时的DP=![]() ,
,
∵∠B=60°,
∴sin60°=![]() ,解得BD=2,
,解得BD=2,
∵D为BC的中点,
∴BC=4,连接AD,
∵△ABC为等边三角形,
∴AD⊥BC,
∴sin60°=![]() ,
,
∴AD=2![]() ,∴S△ABC=
,∴S△ABC=![]() ×4×2
×4×2![]() =4
=4![]() .
.
故选D.
“点睛”本题通过函数图象把动点带来的最小值进行了呈现,正确理解P点运动到何处时DP长最小是关键,同时也考查了3对函数的观察,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目