题目内容
【题目】如图，菱形
的边
轴，垂足为点
，顶点
在第二象限，顶点
在
轴的正半轴上，反比例函数
(
，
)的图像同时经过顶点
、
，若点的横坐标为1，
.则
的值为（ ）
A.
B.3C.
D.5
【答案】C
【解析】
过点D作DF⊥BC于点F，设BC=x，在Rt△DFC中利用勾股定理列方程即可求出x，然后设OB=a，即可表示出C，D的坐标，再代入
可求出a，k的值.
解：过点D作DF⊥BC于点F，
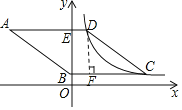
∵点D的横坐标为1，
∴BF=DE=1，
∴DF=BE=3DE=3，
设BC=x，则CD=x，CF=x-1，
在Rt△DFC中，由勾股定理得：
，
∴
，
解得：x=5.
设OB=a，
则点D坐标为(1，a+3)，点C坐标为(5，a)，
∵点D、C在双曲线上
∴1×(a+3)=5a
∴a=
，
∴点C坐标为(5，)，
∴k=
.
故选：C.
【题目】某公司为了更好治理污水质，改善环境，决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 200 | 160 |
经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少1万元．
(1)求a，b的值；
(2)经预算：市治污公司购买污水处理设备的资金不超过78万元，你认为该公司有哪几种购买方案；
(3)在(2)间的条件下，若每月要求处理的污水量不低于1620吨，为了节约资金，请你为该公司设计一种最省钱的购买方案．
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表
单位：环
：
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 10 | 9 | 8 | 8 | 10 | 9 |
乙 | 10 | 10 | 8 | 10 | 7 | 9 |
根据表格中的数据，可计算出甲、乙两人的平均成绩都是9环．
（1）分别计算甲、乙六次测试成绩的方差；
（2）根据数据分析的知识，你认为选______名队员参赛．
