Question

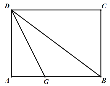
【题目】如图①，在中，点分别在上，且．设的边上的高为，的边上的高为．

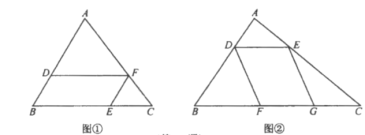
（1）若、的面积分别为3，1，则 ；

（2）设、、四边形的面积分别为，求证：；

（3）如图②，在中，点分别在上，点在上，且， ． 若、、的面积分别为3， 7， 5，求的面积．

Answer 1

【答案】（1） ；（2）见解析；（3）27

【解析】

（1）根据可证∽，根据相似三角形的性质即可得解；

（2）设AD＝a，BD＝b，根据相似三角形的性质利用a、b分别把、表示出来，进而可表示出，然后计算出的结果，即可得证；

（3）将△BDF和△CEG拼接成新△BDH，易得△BDH∽△DAE∽△BAC，且S△BDH＝12，利用相似三角形的性质可得AD:BD＝1:2，进而可得AD：AB＝1:3，再利用相似三角形的面积比等于相似比的平方即可得解．

（1）解：∵，

∴∠AFD＝∠C，∠A＝∠EFC，

∴∽，

∴，

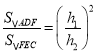∵、的面积分别为3，1，

∴，

∴，

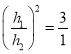故答案为：；

（2）证明：设AD＝a，BD＝b，

∵，

∴∽，∽，

∴，，

∴，，

∴

∴；

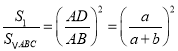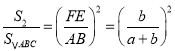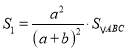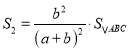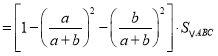
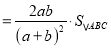
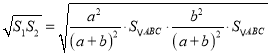
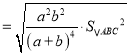
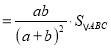
（3）∵，

∴四边形DFGE为平行四边形，

∴DF＝EG，

∴可将△BDF和△CEG拼接成新△BDH，

则△BDH∽△DAE∽△BAC，且S△BDH＝S△BDF＋S△EGC＝7＋5＝12，

∵△BDH∽△DAE，

∴，

∴，

∴，

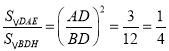∵△DAE∽△BAC，

∴，

∴，

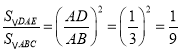∴ΔABC的面积为27．